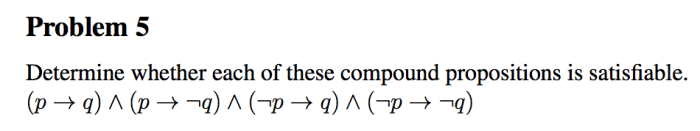Determine whether each of these compound propositions is satisfiable – Determining whether each of these compound propositions is satisfiable is a fundamental concept in propositional logic. It explores the evaluation of compound propositions, formed by combining simpler propositions using logical connectives, to establish their validity or invalidity. This analysis is crucial in automated reasoning, theorem proving, and various applications in computer science.
This comprehensive guide delves into the methods for determining satisfiability, including truth tables, Boolean algebra, and semantic tableaux. It provides examples of satisfiable and unsatisfiable propositions, highlighting the factors that contribute to their respective statuses. Furthermore, it explores the applications of satisfiability in logic, emphasizing its significance in real-world scenarios.
Overview of Satisfiability in Compound Propositions: Determine Whether Each Of These Compound Propositions Is Satisfiable
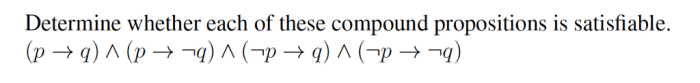
Satisfiability is a fundamental concept in propositional logic that determines whether a compound proposition can be assigned truth values that make it true. A compound proposition is formed by combining multiple propositions using logical operators such as AND, OR, and NOT.
Methods for Determining Satisfiability
There are several methods for determining the satisfiability of compound propositions:
- Truth tables:Truth tables list all possible combinations of truth values for the propositional variables and evaluate the proposition for each combination.
- Boolean algebra:Boolean algebra provides laws and identities that can be used to simplify and analyze compound propositions, making it easier to determine their satisfiability.
- Semantic tableaux:Semantic tableaux is a graphical method that constructs a tree-like structure to represent all possible truth assignments for the propositional variables.
Examples of Satisfiable and Unsatisfiable Propositions, Determine whether each of these compound propositions is satisfiable
Examples of satisfiable compound propositions include:
- (P OR Q) AND (NOT P)
- (P IMPLIES Q) OR (NOT P)
Examples of unsatisfiable compound propositions include:
- (P AND NOT P)
- (P IMPLIES Q) AND (Q IMPLIES NOT P)
Applications of Satisfiability in Logic
Satisfiability plays a crucial role in various applications of logic:
- Automated reasoning and theorem proving:Satisfiability is used to check whether a set of axioms and rules can lead to a contradiction, which is essential for automated reasoning.
- Circuit design and computer science:Satisfiability is used in circuit design to determine whether a circuit can implement a given logical function.
- Real-world applications:Satisfiability is used in areas such as scheduling, resource allocation, and game theory, where it helps determine whether a set of constraints can be simultaneously satisfied.
Detailed FAQs
What is the significance of determining satisfiability in compound propositions?
Determining satisfiability allows us to assess the validity of complex statements, which is essential in automated reasoning, theorem proving, and computer science applications.
How do truth tables contribute to determining satisfiability?
Truth tables provide a systematic way to evaluate all possible combinations of truth values for the propositional variables, enabling us to determine whether a compound proposition is satisfiable or not.
What are the factors that influence the satisfiability of a compound proposition?
The satisfiability of a compound proposition depends on the truth values of its component propositions and the logical connectives used to combine them.