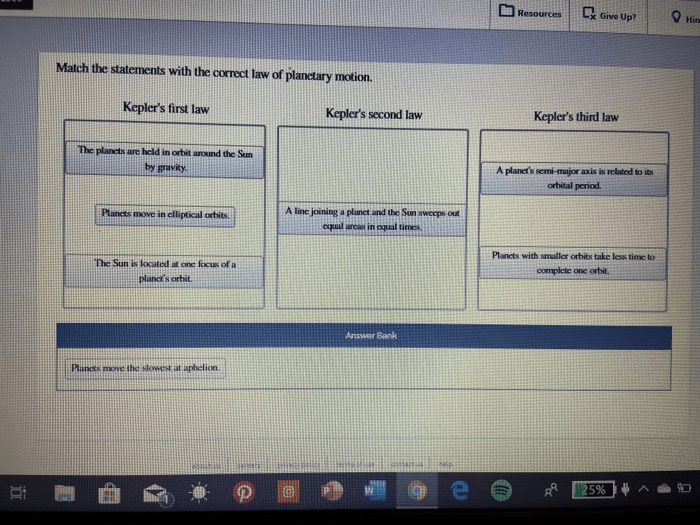
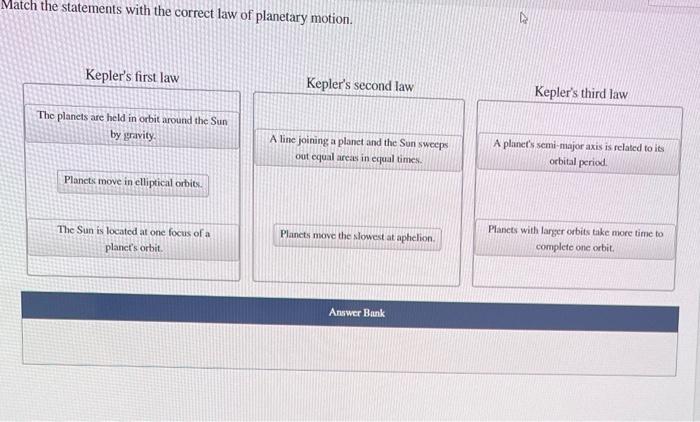
Match the statements with the correct law of planetary motion. As we delve into the celestial mechanics governing the dance of planets around the Sun, we will explore the profound insights offered by Kepler’s and Newton’s laws. Their groundbreaking contributions have illuminated the intricate choreography of our solar system and laid the foundation for our understanding of the cosmos.
Kepler’s laws, with their elegant simplicity, describe the elliptical orbits, constant areal velocities, and harmonic periods of planets. Newton’s laws, on the other hand, provide a deeper understanding of the forces that govern planetary motion, revealing the interplay of gravity, inertia, and centripetal acceleration.
Kepler’s Laws of Planetary Motion
Kepler’s laws of planetary motion are three laws that describe the motion of planets around the Sun. These laws were formulated by Johannes Kepler in the 17th century, based on the observational data collected by Tycho Brahe.
Kepler’s first law states that the orbit of a planet around the Sun is an ellipse, with the Sun located at one of the foci of the ellipse. Kepler’s second law states that a line connecting a planet to the Sun sweeps out equal areas in equal times.
Kepler’s third law states that the square of the period of a planet’s orbit is proportional to the cube of the semi-major axis of its orbit.
These laws have been used to understand the motion of planets in the solar system. For example, Kepler’s first law explains why the planets’ orbits are not circular, but rather elliptical. Kepler’s second law explains why the planets move faster when they are closer to the Sun and slower when they are farther away.
Kepler’s third law can be used to calculate the period of a planet’s orbit, given the semi-major axis of its orbit.
Newton’s Laws of Motion
Newton’s laws of motion are three laws that describe the relationship between the motion of an object and the forces acting on it. These laws were formulated by Isaac Newton in the 17th century.
Newton’s first law states that an object at rest will remain at rest, and an object in motion will remain in motion at constant velocity, unless acted upon by an external force. Newton’s second law states that the acceleration of an object is directly proportional to the net force acting on it, and inversely proportional to its mass.
Newton’s third law states that for every action, there is an equal and opposite reaction.
Newton’s laws of motion can be used to analyze the motion of planets. For example, Newton’s second law can be used to calculate the force of gravity between the Sun and a planet, and to determine the planet’s acceleration due to gravity.
Newton’s third law can be used to explain why the Sun and the planets orbit around each other.
Newton’s laws of motion are limited in their ability to describe the motion of planets. For example, Newton’s laws do not account for the effects of special relativity, which become significant for objects moving at very high speeds.
Applications of Kepler’s and Newton’s Laws

Kepler’s and Newton’s laws have been used in astronomy to understand the motion of planets and other celestial bodies. These laws have been used to predict the motion of planets and to calculate their orbits. Kepler’s and Newton’s laws have also been used to design spacecraft and to plan space missions.
For example, Kepler’s third law has been used to calculate the periods of the planets in the solar system. Newton’s laws of motion have been used to calculate the trajectories of spacecraft and to determine the amount of fuel needed to reach a particular destination.
Extensions of Kepler’s and Newton’s Laws

Kepler’s and Newton’s laws have been extended to account for more complex phenomena. For example, the general theory of relativity, developed by Albert Einstein in the 20th century, provides a more accurate description of the motion of planets and other celestial bodies in strong gravitational fields.
These extensions have improved our understanding of planetary motion. For example, the general theory of relativity explains why the orbit of Mercury is not a perfect ellipse, but rather precesses, or rotates, slowly over time.
However, these extensions are limited in their ability to describe the motion of planets in certain situations. For example, the general theory of relativity does not account for the effects of quantum mechanics, which become significant for objects at very small scales.
Clarifying Questions: Match The Statements With The Correct Law Of Planetary Motion.
What is the significance of Kepler’s Laws?
Kepler’s Laws provide a quantitative description of planetary orbits, enabling astronomers to predict the positions and velocities of planets over time.
How do Newton’s Laws contribute to our understanding of planetary motion?
Newton’s Laws explain the forces that govern planetary motion, revealing the role of gravity and inertia in shaping the trajectories of celestial bodies.
What are the limitations of Newton’s Laws in describing planetary motion?
Newton’s Laws provide an accurate description of planetary motion in most cases, but they do not account for relativistic effects or the influence of non-gravitational forces.